采样（一）：从均匀分布、指数分布和拉普拉斯分布采样

计算机程序的运行是确定性的，即每一步都有一个明确的描述，如何在确定性下生成随机的内容？这似乎是个自相矛盾的问题。

事实上，这个怀疑是对的，在没有外部不确定性的输入下，计算机程序永远以确定性的方式运行。为让计算机程序稳定地生成随机内容，需要稳定的不确定性的输入。而这样做的成本非常高。于是，为何不抛开这个直观思路？

让计算机生成一些看起来随机的确定性序列。易知，伪随机数有一个非常好的优点，可重复。比如我们再训练神经网络时，要初始化大量参数，伪随机数则可以让我们获得同样的初始化参数，从而避免对此训练。

采样和分布变换

采样，可以看做是从给定分布中采集样本，也可以看做是从给定数据集，通过某种策略，采集构造新的数据集的方法。本文讲述从均匀分布采样、从指数分布采样、从正态分布、Laplace分布采样等常见分布采样方法。

首先我们谈谈分布变换，即有已知分布的样本集，通过一定的方法使其变换为符合其他分布的样本集。比如，我现在有一个均匀分布生成器，获得一系列样本$x_1, x_2, \dots, x_n \sim U[0, 1]$，那么通过$g(x)$​​，它如何变换为其他的分布呢？比如变换为正态分布，

$$y_i = g(x_i)$$

这就是分布变换的问题。一般来说，简单的分布容易采样，在获得简单分布的样本后，通过分布变换获得复杂分布的样本。但是对于一般的分布函数，采样方法都不是普遍适用的，因此需要具体分布具体讨论，为每种分布设计最高效的采样方法。

逆变换采样

累积分布函数（CDF）是个单调函数，那么累积分布函数的反函数为，

$$F^{-1}(u) = \inf \left \{ x |F(u) \geq x \right \}$$

如果$u \sim U[0, 1]$，那么$F^{-1}(u)$服从分布$F(x)$。

证明，

$$\begin{align} P(F^{-1}(u) \le x) &= P(u \le F(x)) \newline &= P(u \le y) \Big|_{y = F(x)} \newline &= y|_{y = F(x)} \newline &= F(x) \end{align}$$

这里有一个细节需要说明，由于$u$采样自均匀分布，因此容易知道$P(u \le y) = y$。这一点是以上推导的关键细节。

对于很多分布来说，逆函数$F^{-1}(u)$并不容易计算，因此很多情况下无法直接使用逆变换采样。需要具体分布具体讨论，为每种分布设计最高效的采样方法。下面我们先讨论最简答的均匀分布采样。

均匀分布与线性同余（LCG）

均匀分布表示为，

$$f(x)= \begin{cases}{\frac {1}{b-a}}&\;\mathrm {for} \ a\leq x\leq b,\\ 0&\;\mathrm {otherwise.} \end{cases}$$

均值，

$$\mu = \operatorname{E}[X] = \frac{1}{2} (a + b)$$

方差，

$$\sigma^{2} = \operatorname{Var}(X) = \frac{1}{12}(b-a)^{2}$$

该形式可以改写成已知均值$\mu$和方差$\sigma^2$的均匀分布形式，

$$f(x)= \begin{cases} {\frac {1}{2\sigma {\sqrt {3}}}}&\;{\mbox{if}}-\sigma {\sqrt {3}}\leq x-\mu \leq \sigma {\sqrt {3}}\\0&\;{\text{otherwise.}} \end{cases}$$

考虑对称性，一般会取$b = -a$​，这时均值和方差分别为$0$​和$\frac{a^{2}}{3}$​。如果采样数据只取非负数，那么$a=0$​，这时均值和方差分别是$\frac{b}{2}$​和$\frac{b^{2}}{12}$​​。在有均匀分布$u_i \sim U[0, 1]$​情况下，一般均匀分布有，

$$v_i = a + (b - a) \times u_i$$

Linear congruential generator（LCG）生成伪均匀分布$U[0, 1]$​随机数方法如下，

$$\left\{\begin{array}{l}{x_{i}=a x_{i-1}+b(\bmod m)} \\ {u_{i}=\frac{x_{i}}{m}}\end{array}\right.$$

当 $b=0$​ 时退化成 Lehmer random number generator（LG），是LCG的特例，此处不展开。LCG为什么能成？可以理解为，LCG本身是个周期非常大的函数，周期内的模式是取值均匀且不重复，于是周期内的数呈现正态分布。为获得一个大的周期，$m$需要是一个较大且不可约的正整数。

glibc 中采用的默认参数，

$$\begin{array}{l}{m=2^{31}-1} \\ {a=1103515245} \\ {b=12345}\end{array}$$

通过线性同余方法构建的伪随机数生成器的内部状态可以轻易地由其输出演算得知。

LCG的Python实现如下，

import numpy as np

def lcg(x0, a=1103515245, b=12345, m=2**31-1, normalize=True):
    """线性同余法"""
    while True:
        xt = np.mod(a*x0 + b, m)
        if normalize:
            x = xt / m
        else:
            x = xt
        yield x
        x0 = xt

可视化对比，

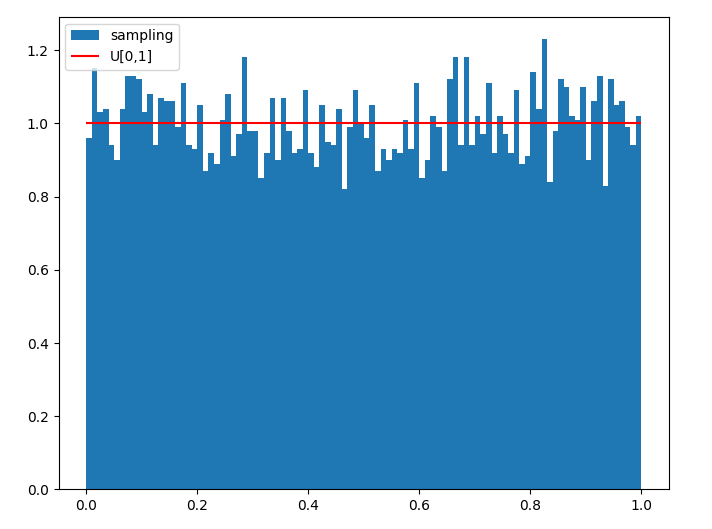
生成均匀分布还有的方法结合位移运算、LFG(Lagged Fibonacci generator)、混沌序列等等。还有一种不太严格的生成技巧，就是生成$f(x) = x$一系列样本，然后shuffle，逐个输出，那么输出样本服从均匀分布。

均匀分布的采样的一个重要应用是随机排列（random permutation），也就是shuffle。Python实现如下，

import numpy as np

def shuffle(x):
    size = len(x)
    for i in range(size-2):
        j = i + np.random.randint(0, size-i)
        x[i], x[j] = x[j], x[i]

均匀分布采样方法作为基础方法，为其他更复杂的分布的采样提供支持。

从指数分布采样

指数分布的概率密度，

$$f(x;\beta )= \begin{cases} \frac {1}{\beta }e^{-x/\beta }&\;x\geq 0,\\ 0& \;x<0. \end{cases}$$

均值和方差分别为$\beta$和$\beta^{2}$。由于指数分布的采样$x \ge 0$，在构造样本时有一定的问题，因此这里不考虑该分布。有些书籍也把指数分布表示为，

$$f(x;\alpha )= \begin{cases} \alpha e^{-\alpha x }&\;x\geq 0,\\ 0& \;x<0. \end{cases}$$

从采样逆变换可知, 如果我们让指数分布的累积分布函数服从均匀分布, 那么其逆函数服从指数分布

$$P(x)=\operatorname{P}(V \leqslant x)=\int_{0}^{x} p(x) \mathrm{d} x=1-\mathrm{e}^{-a x}$$

求逆函数，

$$x=\frac{-\ln (1-u)}{a}$$

因此从均匀分布$U[0, 1]$​中采样一系列的$u_i$​，代入上式获得$x_i$​便服从指数分布。

从Laplace分布采样

拉普拉斯分布的概率密度，

$$f(x\mid \mu ,b)={\frac {1}{2b}}\exp \left(-{\frac {|x-\mu |}{b}}\right)\,$$

均值和方差分别为$\mu, 2b^{2}$​。其累计分布函数也很容易计算，只不过是分步而已，

$$\begin{align} F(x) &\;= \int_{-\infty}^x \!\!f(u)\,\mathrm{d}u \newline &= \begin{cases} \frac12 \exp \left( \frac{x-\mu}{b} \right) &\; \mbox{if }x < \mu \\ 1-\frac12 \exp \left( -\frac{x-\mu}{b} \right) &\; \mbox{if }x \geq \mu \end{cases} \\ &\;=\tfrac{1}{2} + \tfrac{1}{2} \operatorname{sign}(x-\mu) \left(1-\exp \left(-\frac{|x-\mu|}{b} \right ) \right ). \end{align}$$

解得逆函数，

$$F^{-1}(u) = \mu - b\,\operatorname{sign}(u-0.5)\,\ln(1 - 2|u-0.5|)$$

因此从均匀分布$U[0, 1]$中采样一系列的$u_i$，代入上式获得$x_i$​便服从Laplace分布。这里的技巧是先把指数部分解出来，然后再解符号函数部分。

实现

均匀分布、指数分布和拉普拉斯分布的采样方法的实现更新到：

• sampling-from-distribution，可能会根据需要持续更新~

总结

本文介绍了均匀分布、指数分布和拉普拉斯分布的采样方法。

转载请包括本文地址：https://allenwind.github.io/blog/10342
更多文章请参考：https://allenwind.github.io/blog/archives/