从函数光滑近似的角度统一理解激活函数

神经网络强大的表示能力应该归功于网络模型中的激活函数，深度学习中，很多数学形式其实都是光滑逼近的结果。比如激活函数，sigmoid、swish、gelu、softplus，这里从光滑近似的角度统一理解激活函数。

更新：Transformer使用的激活函数GELU。

关于激活函数

神经网络中激活函数的作用：

• 输出层，获得概率意义
• 中间层，产生非线性
• 门机制，如LSTM，信息筛选

激活函数作为输出层，获得概率意义；作为中间层，产生非线性，这些接下来会谈到。这里简单说说作为门机制的激活函数，比如以下网络模型，

$$\begin{align} f(\boldsymbol{x}) &= \operatorname{Dense}(\boldsymbol{x}) \otimes \sigma(\operatorname{Dense}(x)) \\ &= (\boldsymbol{W}_{1}\boldsymbol{x} + \boldsymbol{b}_{1}) \otimes \sigma((\boldsymbol{W}_{2}\boldsymbol{x} + \boldsymbol{b}_{2})) \end{align}$$

称为Gated Linear Units (GLU)，这里激活函数$\sigma(x)$​起到门控的作用。整体上看是一种swish形式的门机制。

激活函数的设计关注如下几点：

• 非线性，产生非线性
• 光滑性，以便求梯度
• 线性区，以便在一定范围内保持输出的均值（0中心）与方差统计特征不漂移
• 活性范围，关系到下层和输出
• 非饱和性
• 计算性能，计算复杂度不能太大

对于第三点，这里展开说说。所谓的线性区是要求激活函数在自变量$x$​取值一定范围内，满足

$$S(x) \approx x'$$

这样，输入$x$和输出$x’$​的均值与方差统计特征的变化不大，以保证网络学习的稳定。

关于次梯度，例如RELU激活函数在$x=0$​处不可导，那么是不是对于深度学习模型来说就无法进行误差逆向传播优化？

事实上，在工程上，有一种叫做次梯度的解决方案。就以RELU函数为例，当$x \gt 0$时，梯度为1，当$x \lt 0$时梯度为0。而0这个位置不存在梯度，而次梯度即选择$[0, 1]$区间中的任意值。在实现时，一般会选择一个区间内的固定值。

逼近0-1函数

Heaviside step函数，

$$\begin{align} H(x) &= \frac {d}{dx}\max\{0, x\} \newline &= \begin{cases} 1,&\;x>0\\ 0,&\;x\leq 0 \end{cases} \end{align}$$

在深度学习中其意义是，如果logit取值为负半轴，则把类别判别为负类（0），如果取值为正半轴，则把类别判别为正类（+1）。另外，从生物学上看，$H(x)$可以直接描述神经元的激活或非激活状态，或者说是一个开关，要么开，要么关。但是$H(x)$并不光滑，对于模型训练来说，寻找其光滑逼近版本相当重要。

这个取值可以改为$1,-1$​，即，

$$\begin{align} H(x) &= \begin{cases} +1,&\;x>0\\ -1,&\;x\leq 0 \end{cases} \end{align}$$

这个函数不可导，模型优化困难。考虑到

$$\displaystyle \operatorname {sign}(x) ={\begin{cases}-1&\;{\text{if }}x<0,\\0&\;{\text{if }}x=0,\\1&\;{\text{if }}x>0.\end{cases}}$$

如果规定$H(0) = \frac{1}{2}$，那么有$H(x) = \frac{1}{2}[1 + \operatorname{sign}(x)]$。​

当$x \ne 0$时，$H(x)$可以用$|x|$表示，

$$H(x)=\frac {x+|x|}{2x}$$

根据$H(x)$​的分段特性可以为均匀分布的概率密度函数提供紧凑的表达形式，如下

$$f(x)={\frac {\operatorname {H} (x-a)-\operatorname {H} (x-b)}{b-a}}$$

$H(x)$​​本身难计算梯度，其梯度是一个非常特殊的函数狄拉克函数$\delta(x)$​，

$$\delta (x)={\frac {d}{dx}}H(x)$$

为此，应用于深度学习需要其光滑版本。以sigmoid为首的很多激活函数就是逼近$H(x)$的光滑版本。

sigmoid

对$H(x)$​函数的逼近是寻找一个S型函数且区间在$(0, 1)$或$(-1, 1)$，最常见的是$\sigma(x)$函数，

$$f(x)=\sigma(x)=\frac{1}{1 + e^{-x}}$$

在Sigmoid函数导出的另外一个角度中我们知道，$\sigma(x)$函数来说$\max(x)$的光滑逼近$ \ln(1 + e^x)$的梯度，

$$\begin{align} H(x) &= \frac {d}{dx}\max\{0, x\} \newline &\approx \frac {d}{dx} \ln(1 + e^x) \newline &= \frac{e^x}{1 + e^x} \newline &= \frac{1}{1 + e^{-x}} \newline &= \sigma(x) \end{align}$$

可以用$\tanh(x)$来表示，

$$\sigma(x) = \frac{1}{2}\left(\tanh \frac{x}{2} + 1\right)$$

这两个激活函数都存在当$x$很大时梯度饱和，即接近0。

tanh

注意到，$\tanh (x)$可以用$\sigma(x)$表示

$$\tanh (x) = \frac{e^{x}-e^{-x}}{e^{x}+e^{-x}} = 2\sigma(2x) - 1$$

是$\sigma(x)$​的一个仿射变换，因此还是S型函数，不过取值区间变为$(-1, 1)$。

$\tanh(x)$与$\sigma(x)$的梯度与自身相关，即：

$$(\tanh(x))' = 1 - \tanh^2(x) \\ \sigma'(x) = \sigma(x) (1 - \sigma(x))$$

这个性质很有用，可以复用已有的计算结果。

softsign

softsign激活函数为，

$$\displaystyle f(x)={\frac {x}{1+|x|}}$$

该激活函数来自$\operatorname{sign}(x)$的近似，

$$\operatorname{sign}(x) = \frac{x}{|x|}\approx \frac{x}{\beta + |x|} \approx \frac{x}{1 + |x|}$$

softsign激活函数可以推广开来，

$$\displaystyle f_k(x)={\frac {x}{(1+|x|^k)^{\frac{1}{k}}}}$$

按照类似的思路，有，

$$\operatorname{sign}(x) = \frac{x}{|x|} = \frac{x}{\ln e^{|x|}} \approx \frac{x}{\ln( e^{x} + e^{-x})}$$

激活函数用S型函数逼近0-1阶跃函数的好处是在$x$较小时，有

$$S(x) \approx x$$

例如$\tanh(x) \approx x$，这样通过激活函数输出后，均值和方差大致保存不变，这样便于模型的训练和优化。

逼近RELU函数

RELU函数，

$$\begin{align} \operatorname{relu}(x) &= \max(0, x) \newline &= x \times H(x) \newline &=\left\{\begin{array}{ll}{0} & {\text { for } x \leq 0} \\ {x} & {\text { for } x>0}\end{array}\right. \end{align}$$

从神经元的角度看，RELU激活函数描述两种状态：

• 非激活状态，即负半轴
• 激活状态的激活程度，即正半轴，且不具有饱和性

用一句话来说就是单边抑制宽兴奋边界，这是有生物学合理性。但是从数学角度看，RELU的定义非光滑，不利于优化。

RELU激活函数的图形呈现无上界有下界，但有一个严重的问题，即死区，当网络输出值在负半轴时，非激活状态一直延续到后层。解决方案有：

• 平滑RELU，平滑$H(x)$或平滑整体$x \times H(x)$，也就是寻找$\max(0, x)$的光滑版本，如果是前者，则寻找一个S型函数逼近即可。
• 分段化RELU，使其负半轴取值不为0

简而言之，如果找到$H(x)$的光滑逼近函数，那么也就找到$\operatorname{relu}(x)$的光滑逼近；如果找到$\max(0, x)$的光滑逼近，那么也找到$\operatorname{relu}(x)$​​的光滑。

RELU改进应该满足一下几点：

• 平滑RELU的函数应该连续可导
• 平滑RELU的函数负半轴应该非单调，以便增加非线性
• 平滑RELU的函数，在$x$​较小时，$R_s(x) \approx x$

RELU改进方案：

• Noisy ReLU
• Softplus
• ELU
• SELU
• GELU

下面我们来谈谈它们的设计思路。

Noisy ReLU

考虑添加噪声

$$f(x)=\max(0,x+Y), \quad Y\sim {\mathcal {N}}(0,\sigma^2)$$

这个激活函数的出发点是增加鲁棒性。

ELU & SELU

改变RELU死区问题的一个思路是分段化，负半轴通过一定技巧避免其取值为0，常见有ELU函数，

$$f(\alpha, x)=\left\{\begin{array}{ll}{\alpha\left(e^{x}-1\right)} & {\text { for } x \leq 0} \\ {x} & {\text { for } x>0}\end{array}\right.$$

其中 $\alpha \ge 0$​ 。

SELU函数，

$$\begin{array}{ll}{f(x, \alpha)=\lambda\left\{\begin{array}{ll}{\alpha\left(e^{x}-1\right)} & {\text { for } x<0} \\ {x} & {\text { for } x \geq 0}\end{array}\right.} \\ \end{array}$$

其中$\lambda=1.0507,\alpha=1.67326$​​ ，这两个参数用来微调ELU激活函数。SELU激活函数来自论文Self-Normalizing Neural Networks。论文提到该激活函数不使用Normalization手段能够自动归一化。

Softplus

Softplus函数为，

$$\displaystyle f(x)=\ln(1+e^{x})$$

我们都知道Logsumexp是max的光滑近似，

$$\begin{align}\underset{\alpha \rightarrow \infty}{\lim} \frac{1}{\alpha} \log( \sum_{i=1}^{n}e^{\alpha x_{i}}) = \max(x_{1},\dots,x_{n})\end{align}$$

因此取$n=2, x_1 = x, x_2 = 0, \alpha=1$​有，

$$\begin{align} \operatorname{relu}(x) &= \max\{0, x \} \newline &\le \ln( 1 + e^{x}) \end{align}$$

因为是 RELU 的光滑化版本，故称为 SmoothReLU。这里Logsumexp可以认为是Softplus的推广。

此外，还有积分思路，

$$\begin{align} \operatorname{relu}(x) &= \left\{\begin{array}{ll}{0} & {\text { for } x \leq 0} \\ {x} & {\text { for } x>0}\end{array}\right. \newline &= \max\{0, x\} \newline &= \int_{-\infty}^{x} H(x) \; dx \newline &\approx \int_{-\infty}^{x} \frac{1}{1 + e^{-2kx}} \; dx \newline &= \frac{1}{2k} \ln( 1 + e^{2kx}) \end{align}$$

取$k=\frac{1}{2}$​得Softplus函数。Softplus激活函数是单调的，负半轴无法提供更多的非线性功能。

Swish

过去的一篇文章Google的激活函数Swish是怎么设计出来的？也分析过Swish的导出，可参看。Swish函数为，

$$f(x) = x\sigma(x)$$

$\sigma(x)$可以看做是一个门，控制$x$​​的输出。易知，

$$\begin{align} \operatorname{relu}(x) &= \max\{0, x \} \newline &= x \times H(x) \end{align}$$

然后注意到Heaviside step函数$H(x)$可以用$\tanh(x)$逼近，即，

$$\begin{align} H(x) &= \frac {d}{dx}\max\{0, x\} \newline &= \begin{cases} 1,&\;x>0\\ 0,&\;x\leq 0 \end{cases} \newline &\approx \frac{1}{2} + \frac{1}{2} \tanh(kx) \newline &= \frac{1}{1 + e^{-2kx}} \end{align}$$

我们取$k=\frac{1}{2}$​，有基于$H(x)$​光滑逼近的$\operatorname{relu}(x) $​近似，

$$\operatorname{relu}(x) \approx \frac{x}{1 + e^{-x}} = x \sigma(x)$$

Mish

后面的文章更新了Mish激活函数的分析，见Mish激活函数的设计思路。

GELU

GELU，全称为Gaussian Error Linear Unit，也算是RELU的变种。对比一下和RELU的区别，

首先我们知道误差函数$\operatorname{erf}(x)$，

$$\operatorname{erf}(x) = \frac{1}{\sqrt{\pi}}\int_{-x}^{x}e^{-t^{2}}dt = \frac{2}{\sqrt{\pi}}\int_{0}^{x}e^{-t^{2}}dt$$

是一个像logistics函数图像一样的函数，易证$\operatorname{erf}(\frac{x}{\sqrt{2}}) \in (-1, 1)$​​，函数图像如下，

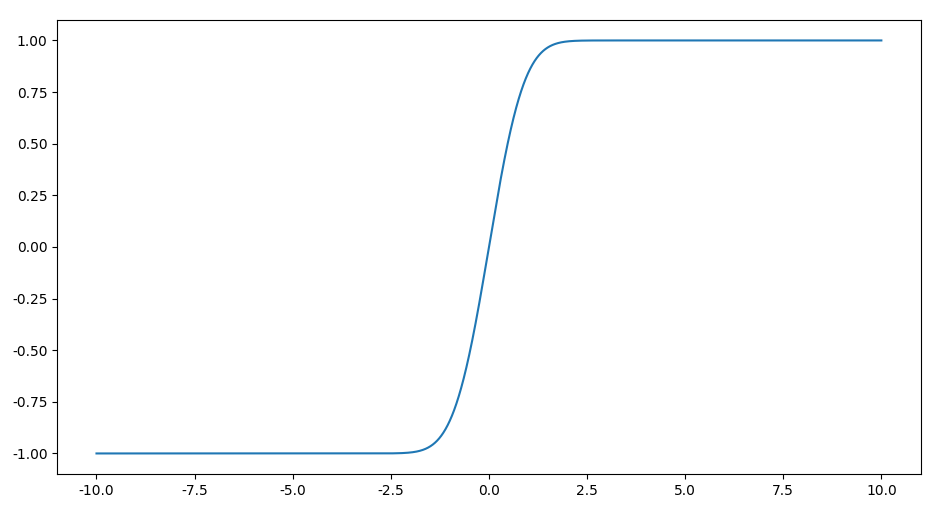
可以变换到$(0, 1)$​​区间，即$\frac{1}{2} \Big[ 1 + \operatorname{erf}(\frac{x}{\sqrt{2}}) \Big]$​​，是$H(x)$的光滑近似。有趣的是，标准正态分布的累积分布函数可以用$\operatorname{erf}(x)$​​表示，

$$\Phi(x) = \frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{x} e^{\frac{-t^2}{2}} dt = \frac{1}{2} \Big( 1 + \operatorname{erf}(\frac{x}{\sqrt{2}}) \Big) \in (0, 1)$$

GELU可以由标准正态分布的累积分布函数表示，

$$\operatorname{GELU}(x)=x P(X \leq x)=x \Phi(x)$$

因此有，

$$\operatorname{GELU}(x) \approx \frac{x}{2}\left[1 + \text{erf}\left(\frac{x}{\sqrt{2}}\right)\right]$$

由于$\frac{1}{2} \Big[ 1 + \operatorname{erf}(\frac{x}{\sqrt{2}}) \Big]$​，是$H(x)$​​的光滑近似，于是有，

$$\begin{align} \operatorname{relu}(x) &= \max\{0, x \} \newline &= x \times H(x) \newline &\approx x \times \frac{1}{2} \Big[ 1 + \operatorname{erf}(\frac{x}{\sqrt{2}}) \Big] \newline &= x \Phi(x) \newline &= \operatorname{GELU}(x) \end{align}$$

论文Gaussian Error Linear Units (GELUs)中还有如下结论近似$\operatorname{GELU}(x)$，

$$\operatorname{GELU}(x) \approx \frac{x}{2} \left[1 + \tanh\left(\sqrt{\frac{2}{\pi}}\left(x + 0.044715 x^3\right)\right)\right]$$

测试该函数可以用scipy.special.erf，有些框架并没有提供该函数则会使用近似。也就有，

$$\operatorname{erf}(\frac{x}{\sqrt{2}}) \approx \tanh \left[ \sqrt{\frac{2}{\pi}} (x + 0.044715x^3)\right]$$

其实该近似挺符合我们的数学直觉，$\operatorname{erf}(\frac{x}{\sqrt{2}})$本身是S型函数，$\tanh(x)$也是S型函数，因此，

$$\tanh(ax + bx^3)$$

形式的函数也是S型函数，通过$a,b$参数控制S形状可以逼近$\operatorname{erf}(\frac{x}{\sqrt{2}})$​​。

自行构造

光滑近似的构造是相当灵活的，可以自行构造。例如根据

$$|x-y| \approx \sqrt{(x-y)^2 + \alpha}$$

有，

$$\begin{align} \max(x,y) &= \frac{|x+y|+|x-y|}{2} \newline &= \frac{1}{2}\Big((x + y) + \sqrt{ (x - y)^2} \Big) \newline &\approx \frac{1}{2}\Big((x + y) + \sqrt{ (x - y)^2 + \alpha} \Big) ,\quad \alpha \to 0 \end{align}$$

于是relu激活函数有近似，

$$\begin{align} \operatorname{relu}(x) &= \max(0, x) \newline &\approx \frac{1}{2}\Big(x + \sqrt{ x^2 + \alpha} \Big) \end{align}$$

这里$\alpha \to 0$取等号，实践中可以取$\alpha = 0.01$​。​

类似地，考虑$|x| \approx \sqrt{x^2 + \alpha}$，有​

$$\begin{align} H(x) &= \begin{cases} 1,&\;x>0\\ 0,&\;x\leq 0 \end{cases} \newline &= \begin{cases} \frac{1}{2}\big(\frac{x}{|x|} + 1\big),&\;x \ne 0\\ 0,&\;x = 0 \end{cases} \newline &\approx \frac{1}{2}\Big(\frac{x}{\sqrt{x^2 + \alpha}} + 1\Big) \end{align}$$

其中$\alpha$​是一个可以小的数，如$\alpha = 0.1$​​。可视化图像如下，

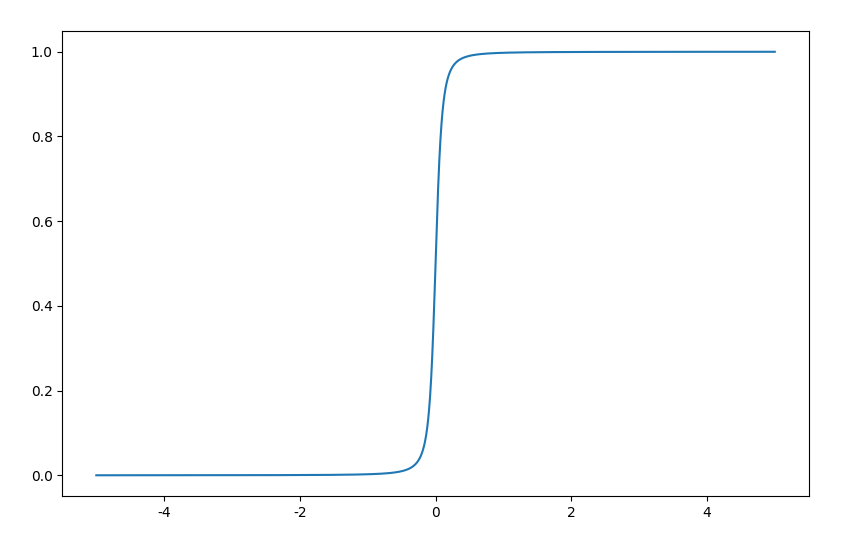
考虑到$\operatorname{relu}(x) = x \times H(x)$，只要找到$H(x)$的光滑近似，自然就有$\operatorname{relu}(x)$的光滑近似。因此，也有，

$$\begin{align} \operatorname{relu}(x) &= x \times H(x) \newline &\approx \frac{x}{2}\Big(\frac{x}{\sqrt{x^2 + \alpha}} + 1\Big) \end{align}$$

诸如此类，等等。

补充：更多自行设计激活函数的思路可看最新文章天马行空：设计自己的激活函数。

总结

本文从光滑近似的角度统一理解激活函数。函数光滑近似能够创造更多的性能优良的激活函数。

sigmoid类激活函数的本质是平滑$H(x)$，relu类函数的本质是平滑$\operatorname{relu}(x) = x \times H(x)$。​

对$\operatorname{relu}(x) = \max(0, x) = x \times H(x)$​的光滑近似能够创造更多的激活函数，光滑近似思路有两种，平滑$H(x)$​或平滑整体$x \times H(x)$​​，如果是前者，则寻找一个S型函数逼近即可，不同的逼近方式获得不同的激活函数。

转载请包括本文地址：https://allenwind.github.io/blog/10705
更多文章请参考：https://allenwind.github.io/blog/archives/